

Unlike the mathematically unique models, however, the gamut of usable coding languages and interfaces provides a plurality of valid ways to implement and distribute Wulff computational tools, each with advantages and limitations. The development of computer-based interfaces implementing shape models is much newer than the models themselves and buoyed by both the open-source movement and the wide availability of computing resources.
#Ipicture of a cuboctahedron flattened software#
for the common face-centered cubic (FCC) metals, often relies on software development for the visualization and quantification of shapes. These mathematical models are all general, and specific crystallographic implementation, e.g. Extensions to this purely thermodynamic, single crystal Wulff construction have been developed over the past decades to incorporate twinning , alloys , substrate(s) , and kinetic effects such that most shapes and conditions can now be modelled.
#Ipicture of a cuboctahedron flattened free#
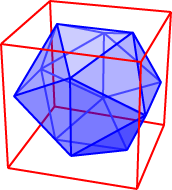
a plot of the orientation-dependent surface free energy (surface energy for simplicity subsequently). According to this approach, the equilibrium shape of single crystals is determined from a gamma plot, i.e. This was formalized in 1901 by Wulff into the “Wulff construction,” sometimes referred to as the “classic” or “thermodynamic” Wulff construction. The thermodynamic equilibrium shape of a nanocrystal, the simplest one to model, is governed by surface energy minimisation, as determined by Gibbs in 1873 . This steady rise in interest in Wulff construction and nanoparticle shape is poised to continue as scientists explore unusual crystal systems and ever-increasing nanoparticle complexity. Figure 1 shows the much smaller number, but similar steady increase, of papers including in their title or abstract the words “nanoparticle”, “shape” and “thermodynamic”, or the words “Wulff construction”. However, only a small fraction of these 10,000s of papers are relevant to nanoparticle shape research.

Marks and Peng showed in 2016 that the number of publications using “nanoparticle” as a keyword increased approximately linearly with time this trend has continued through 2020 (Additional file 1: Fig. Interest in nanocrystal shape and its control has, therefore, followed the trend of interest in nanostructures. Understanding such effects, possible through the various crystal growth models developed over the last century, is key to rationalizing and predicting the shape of crystalline nanoparticles. In bottom-up approaches, thermodynamic and kinetic mechanisms dictate atomic assembly. Unlike in the bulk, the size and shape of nanocrystals has a profound influence on their properties, driving interest and effort in precise control strategies for both top-down fabrication and bottom-up synthesis approaches. Nanocrystals, defined as crystalline particles of size ranging from 1 to 1000 nm, have found a myriad of applications across science and engineering, for instance in optical devices , chemical catalysis , drug delivery , and biological sensors , to name a few. This review provides a guide for scientists looking to model crystal shape in a field where ever-increasingly complex crystal shapes and compositions are required to fulfil the exciting promises of nanotechnology. Finally, a discussion of the scientific applications of shape models to either predict shape or use shape to deduce thermodynamic and/or kinetic parameters is offered, followed by a conclusion. Then, the multitude of published software implementations of these Wulff-based shape models are described in detail, describing their technical aspects, advantages and limitations. In this review, the various mathematical approaches used to model crystal shapes are first overviewed, from the century-old Wulff construction to the year-old (2020) approach to describe supported twinned nanocrystals, together with a discussion and disambiguation of the terminology. The imperative to understand and predict nanocrystal shape led to the development, over several decades, of a large number of mathematical models and, later, their software implementations. Unlike in the bulk, at the nanoscale shape dictates properties.


 0 kommentar(er)
0 kommentar(er)
